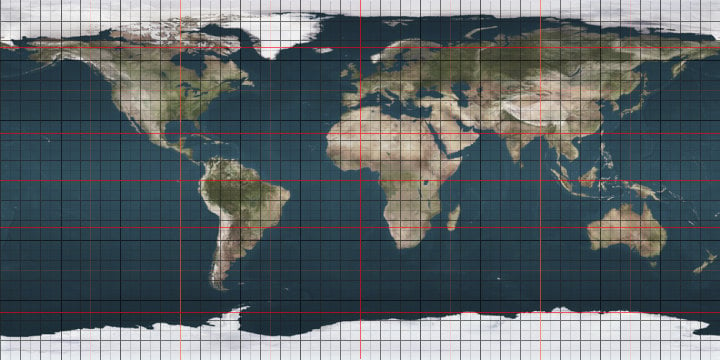
Equator

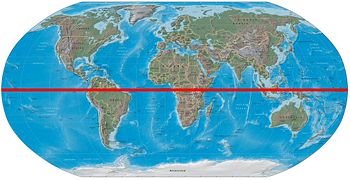
World map showing the line of the equator in red.

The equator is the intersection of the Earth's surface with the plane perpendicular to the Earth's axis of rotation and containing the Earth's center of mass. In more simple language, it is an imaginary line on the Earth's surface that is everywhere equidistant from the North Pole and South Pole. It is from this point that latitude is calculated, in other words, it is the 0° latitude line. This geographic, or terrestrial, Equator divides the Earth into a Northern Hemisphere and a Southern Hemisphere. The equators of other planets and astronomical bodies are defined analogously.

The word "equator" comes from the Latin, circulus aequator diei et noctis, meaning "circle equalizing day and night." This term was originally coined in reference to the Celestial Equator, but has come to mean that which divides a sphere into two equal parts.

While the equator is a significant marker for the geographer, dividing the two hemispheres and providing an important point of calculation, for the sea-going navigator it is simply a line on a map—the point of measurement (previously in the stars) lies in instruments which relate to the earth's magnetic poles.

Geodesy of the equator

The latitude of the equator is, by definition, 0°. The length of Earth's equator is about 40,075 kilometers (24,901.5 mi).

The equator is one of the five main circles of latitude that are based on the relationship between the Earth's axis of rotation and the plane of the Earth's orbit around the sun. It is the only line of latitude which is also a great circle. The imaginary circle obtained when the Earth's equator is projected onto the sky is called the celestial equator.

The Sun, in its seasonal movement through the sky, passes directly over the equator twice each year, on the March and September equinoxes. At the equator, the rays of the sun are perpendicular to the surface of the earth on these dates.

Places on the equator experience the quickest rates of sunrise and sunset in the world. Such places also have a theoretical constant 12 hours of day and night throughout the year (in practice there are variations of a few minutes due to the effects of atmospheric refraction and because sunrise and sunset are measured from the time the edge of the Sun's disc is on the horizon, rather than its center). North or south of the equator day length increasingly varies with the seasons.

The Earth bulges slightly at the equator. It has an average diameter of 12,750 kilometers (7,922 mi), but at the equator the diameter is approximately 43 kilometers (27 mi) greater.

Locations near the equator are good sites for spaceports, such as the Guiana Space Centre in Kourou, French Guiana, as they are already moving faster than any other point on the Earth due to the Earth's rotation, and the added velocity reduces the amount of fuel needed to launch spacecraft. Spacecraft launched in this manner must launch to the east to use this effect.

For high precision work, the equator is not quite as fixed as the above discussion implies. The true equatorial plane must always be perpendicular to the Earth's spin axis. Although this axis is relatively stable, its position wanders in approximately a 9 meters (30 ft) radius circular motion each year. Thus, the true equator moves slightly. This, however, is only important for detailed scientific studies. The effect is quite small, and the width of a line marking the equator on almost any map will be much wider than the error.

Equatorial climate

Temperatures near the equator are high year round with the exception for periods during the wet season and at higher altitudes. In many tropical regions people identify two seasons: Wet and dry. However, most places close to the equator are wet throughout the year, and seasons can vary depending on a variety of factors including elevation and proximity to an ocean. The rainy and humid conditions mean that the equatorial climate is not the hottest in the world.

The surface of the Earth at the equator is mostly ocean. The highest point on the equator is 4,690 meters (15,387 ft), at 00°00′00″S, 77°59′31″W, on the south slopes of Volcán Cayambe (summit 5,790 meters (18,996 ft)) in Ecuador. This is a short distance above the snow line, and this point and its immediate vicinity form the only section of the equator where snow lies on the ground.

Equatorial countries and territories

In tourist areas, the equator is often marked on the sides of roads.

The equator marked as it crosses Ilhéu das Rolas, in São Tomé and Príncipe.

The equator traverses the land and/or territorial waters of 14 countries. Starting at the Prime Meridian and heading eastward, the equator passes through:

long	Country, territory or sea	Notes
0°	Atlantic Ocean	Gulf of Guinea
7° E	São Tomé and Príncipe	Ilhéu das Rolas
8°	Atlantic Ocean	Gulf of Guinea
10°	Gabon
15°	Republic of the Congo
20°	Democratic Republic of the Congo
30°	Uganda
33°	Lake Victoria
35° 40°	Kenya
41°	Somalia
43° 50° 60° 70°	Indian Ocean
73°	Maldives	Passing between Gaafu Dhaalu Atoll and Gnaviyani Atoll
80° 90°	Indian Ocean
100°	Indonesia	The Batu Islands, Sumatra and the Lingga Islands
105°	Indian Ocean	Karimata Strait
110°	Indonesia	Borneo
118°	Indian Ocean	Makassar Strait
120°	Indonesia	Sulawesi
121°	Indian Ocean	Gulf of Tomini
125°	Indian Ocean	Molucca Sea
127°	Indonesia	Kayoa and Halmahera islands
128°	Pacific Ocean	Halmahera Sea
130°	Indonesia	Gebe Island
140° 150° 160°	Pacific Ocean
173°	Kiribati	Misses every island, passing between Aranuka and Nonouti Atolls
180°	Pacific Ocean
176° W	United States Minor Outlying Islands	Baker Island—passes through territorial waters The equator also passes through the exclusive economic zones around Howland Island and Jarvis Island, but not through their territorial waters
170° 160° 150° 140° 130° 120° 110° 100°	Pacific Ocean
90°	Ecuador	Isabela Island in the Galápagos Islands
88°	Pacific Ocean
80°	Ecuador	The literal translation of Ecuador's official name is "Republic of the Equator"
70°	Colombia	It intersects the country through an Amazon jungle area.
60° 50°	Brazil	Including some islands in the mouth of the Amazon River
40° 30° 20° 10°	Atlantic Ocean

Despite its name, no part of Equatorial Guinea's territory lies on the equator. However, its island of Annobón is about 156 kilometers (100 mi) south of the equator, and the rest of the country lies to the north. The country that comes closest to the equator without actually touching it is Peru.

Length of the equator

The equator is modeled exactly in two widely used standards as a circle of radius an integer number of meters. In 1976, the International Astronomical Union (IAU) standardized this radius as 6,378,140 meters (20,925,656 ft), subsequently refined by the International Union of Geodesy and Geophysics (IUGG) to 6,378,137 meters (20,925,646 ft) and adopted in World Geodetic System (WGS-84), though the yet more recent IAU-2000 has retained the old IAU-1976 value. In either case, the length of the equator is by definition exactly 2π times the given standard, which to the nearest millimeter is 40,075,016.686 meters (131,479,713.54 ft) in WGS-84 and 40,075,035.535 meters (131,479,775.38 ft) in IAU-1976 and IAU-2000.^[1]

The geographical mile is defined as one arc minute of the equator, and therefore has different values depending on which standard equator is used, namely 1,855.3248 meters (6,087.024 ft) or 1,855.3257 meters (6,087.027 ft) for respectively WGS-84 and IAU-2000, a difference of nearly a millimeter.

The earth is standardly modeled as a sphere flattened about 0.336 percent along its axis. This results in the equator being about 0.16 percent longer than a meridian (as a great circle passing through the two poles). The IUGG standard meridian is to the nearest millimeter 40,007,862.917 meters (131,259,392.77 ft), one arc minute of which is 1,852.216 meters (6,076.82 ft), explaining the International System of Units (SI) standardization of the nautical mile as 1,852 meters (6,076 ft), more than 3 meters (10 ft) short of the geographical mile.

Celestial equator

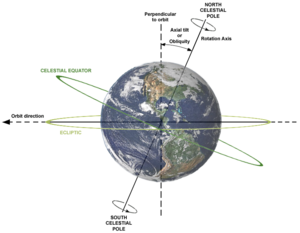
The celestial equator is inclined by ~23.5° to the ecliptic plane. The image shows the relations between Earth's axial tilt (or obliquity), rotation axis and plane of orbit.

The celestial equator is a great circle on the imaginary celestial sphere, in the same plane as the Earth's equator. In other words, it is a projection of the terrestrial equator out into space. As result of the Earth's axial tilt, the celestial equator is inclined by ~23.5° with respect to the ecliptic plane.

An observer standing on the Earth's equator visualizes the celestial equator as a semicircle passing directly overhead through the zenith. As the observer moves north (or south), the celestial equator tilts towards the southern (or northern) horizon. The celestial equator is defined to be infinitely distant (since it is on the celestial sphere); thus the observer always sees the ends of the semicircle disappear over the horizon exactly due east and due west, regardless of the observer's position on Earth. (At the poles, though, the celestial equator would be parallel to the horizon.)

Celestial objects near the celestial equator are visible worldwide, but they culminate the highest in the sky in the tropics. The celestial equator passes through these constellations:

Pisces
Cetus
Taurus
Eridanus
Orion

Monoceros
Canis Minor
Hydra
Sextans
Leo

Virgo
Serpens
Ophiuchus
Aquila
Aquarius

Notes

↑ Although millimeter precision can be important up to the scale of a mile, it has negligible physical significance at the scale of a geographic feature such as the equator. From a computational standpoint, however, millimeter precision or better can be valuable for maintaining consistent results when used in programs for surveying and other applications that require precise measurements. As an overly simple example, if a program were to convert back and forth between the radius and the circumference of the earth sufficiently often while maintaining precision only to a meter each time, errors might accumulate until they became noticeable.

References
ISBN links support NWE through referral fees

Clarke, Thurston. Equator: A Journey. New York: Morrow, 1988. ISBN 978-0688069018.
"Geodetic Reference System 1980 by H. Moritz." Journal of Geodesy. 74 (1) (2000): 128. ISSN 0949-7714.
Rosenberg, Matt. The Equator, Hemispheres, Tropic of Cancer, and Tropic of Capricorn. The New York Times Company-About.com. (April 16, 1999). Retrieved February 12, 2022.
Taff, Laurence G. Computational Spherical Astronomy. New York: Wiley, 1981. ISBN 047106257X.

Credits

New World Encyclopedia writers and editors rewrote and completed the Wikipedia article in accordance with New World Encyclopedia standards. This article abides by terms of the Creative Commons CC-by-sa 3.0 License (CC-by-sa), which may be used and disseminated with proper attribution. Credit is due under the terms of this license that can reference both the New World Encyclopedia contributors and the selfless volunteer contributors of the Wikimedia Foundation. To cite this article click here for a list of acceptable citing formats.The history of earlier contributions by wikipedians is accessible to researchers here:

The history of this article since it was imported to New World Encyclopedia:

History of "Equator"

Note: Some restrictions may apply to use of individual images which are separately licensed.

[1] Although millimeter precision can be important up to the scale of a mile, it has negligible physical significance at the scale of a geographic feature such as the equator. From a computational standpoint, however, millimeter precision or better can be valuable for maintaining consistent results when used in programs for surveying and other applications that require precise measurements. As an overly simple example, if a program were to convert back and forth between the radius and the circumference of the earth sufficiently often while maintaining precision only to a meter each time, errors might accumulate until they became noticeable.

[1]